Motzkin Numbers and RNA Secondary Structures

https://rosalind.info/problems/motz/

ROSALIND | Motzkin Numbers and RNA Secondary Structures

Problem

Figure 1. The 21 distinct ways to form a noncrossing matching on 5 labeled nodes. (Courtesy: Robertd, Wikimedia Commons User)

Figure 2. Two possible noncrossing matchings of basepair edges in the bonding graph corresponding to RNA string UAGCGUGAUCAC.

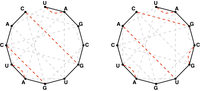
Similarly to our definition of the Catalan numbers, the nn-th Motzkin number mnmn counts the number of ways to form a (not necessarily perfect) noncrossing matching in the complete graph KnKn containing nn nodes. For example, Figure 1 demonstrates that m5=21m5=21. Note in this figure that technically, the "trivial" matching that contains no edges at all is considered to be a matching, because it satisfies the defining condition that no two edges are incident to the same node.

How should we compute the Motzkin numbers? As with Catalan numbers, we will take m0=m1=1m0=m1=1. To calculate mnmn in general, assume that the nodes of KnKn are labeled around the outside of a circle with the integers between 1 and nn, and consider node 1, which may or may not be involved in a matching. If node 1 is not involved in a matching, then there are mn−1mn−1 ways of matching the remaining n−1n−1 nodes. If node 1 is involved in a matching, then say it is matched to node kk: this leaves k−2k−2 nodes on one side of edge {1,k}{1,k} and n−kn−k nodes on the other side; as with the Catalan numbers, no edge can connect the two sides, which gives us mk−2⋅mn−kmk−2⋅mn−k ways of matching the remaining edges. Allowing kk to vary between 22 and nn yields the following recurrence relation for the Motzkin numbers: mn=mn−1+∑nk=2mk−2⋅mn−kmn=mn−1+∑k=2nmk−2⋅mn−k.

To count all possible secondary structures of a given RNA string that do not contain pseudoknots, we need to modify the Motzkin recurrence so that it counts only matchings of basepair edges in the bonding graph corresponding to the RNA string; see Figure 2.

Given: An RNA string ss of length at most 300 bp.

Return: The total number of noncrossing matchings of basepair edges in the bonding graph of ss, modulo 1,000,000.

Sample Dataset

>Rosalind_57
AUAU

Sample Output

7

 

 이 문제는 주어진 RNA의 Motzikin 수를 출력하는 문제이다. Motzkin수는 카탈란수와 달리 부분적으로나마 짝이 지어진것도 경우의 수로 친다는 점이다. 그러므로 기본적으로 Motzkin 수는 카탈란 수처럼 완벽하게 짝이 지어지는 경우의 수만 세지 않는다. 그리고 1개,2개... 짝이 지어진 것도 고려해야 하므로 피보나치 수열처럼 더 짧은 서열에서의 경우의 수도 더해야 한다. 카탈란수를 구하는 알고리즘에 저 두가지만 유의해서 고치면 풀 수 있는 문제이다.

from Bio import SeqIO

def finding_mot(s,node,mot_memo):
    if node<=1:
        return 1
    if mot_memo.get((s,node),0):
        return mot_memo[(s,node)]
    Cn=finding_mot(s[1:],node-1,mot_memo)#앞의 경우의 수

    for k in range(1,node):
        if (s[0],s[k]) in [('A','U'),('U','A'),('C','G'),('G','C')]:#짝만 지어지면
            Cn+=finding_mot(s[1:k],k-1,mot_memo)*finding_mot(s[k+1:len(s)],node-k-1,mot_memo)
    
    mot_memo[(s,node)] = Cn

    return Cn

if __name__=='__main__':
    with open(r'파일경로','r') as fa:
        S=next(SeqIO.parse(fa,'fasta')).seq

mot_memo={}
node=len(S)

mot=finding_mot(S,node,mot_memo)
print(mot%1000000)