Catalan Numbers and RNA Secondary Structures(다시 풀기)

https://rosalind.info/problems/cat/

ROSALIND | Catalan Numbers and RNA Secondary Structures

Problem

Figure 3. The only two noncrossing perfect matchings of basepair edges (shown in red) for the RNA string UAGCGUGAUCAC.

Figure 4. All possible noncrossing perfect matchings in complete graphs on 2, 4, 6, and 8 nodes; the total number of such matchings are 1, 2, 5, and 14, respectively.

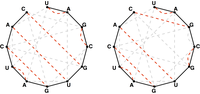
A matching in a graph is noncrossing if none of its edges cross each other. If we assume that the nn nodes of this graph are arranged around a circle, and if we label these nodes with positive integers between 1 and nn, then a matching is noncrossing as long as there are not edges {i,j}{i,j} and {k,l}{k,l} such that i<k<j<li<k<j<l.

A noncrossing matching of basepair edges in the bonding graph corresponding to an RNA string will correspond to a possible secondary structure of the underlying RNA strand that lacks pseudoknots, as shown in Figure 3.

In this problem, we will consider counting noncrossing perfect matchings of basepair edges. As a motivating example of how to count noncrossing perfect matchings, let cncn denote the number of noncrossing perfect matchings in the complete graph K2nK2n. After setting c0=1c0=1, we can see that c1c1 should equal 1 as well. As for the case of a general nn, say that the nodes of K2nK2n are labeled with the positive integers from 1 to 2n2n. We can join node 1 to any of the remaining 2n−12n−1 nodes; yet once we have chosen this node (say mm), we cannot add another edge to the matching that crosses the edge {1,m}{1,m}. As a result, we must match all the edges on one side of {1,m}{1,m} to each other. This requirement forces mm to be even, so that we can write m=2km=2k for some positive integer kk.

There are 2k−22k−2 nodes on one side of {1,m}{1,m} and 2n−2k2n−2k nodes on the other side of {1,m}{1,m}, so that in turn there will be ck−1⋅cn−kck−1⋅cn−k different ways of forming a perfect matching on the remaining nodes of K2nK2n. If we let mm vary over all possible n−1n−1 choices of even numbers between 1 and 2n2n, then we obtain the recurrence relation cn=∑nk=1ck−1⋅cn−kcn=∑k=1nck−1⋅cn−k. The resulting numbers cncn counting noncrossing perfect matchings in K2nK2n are called the Catalan numbers, and they appear in a huge number of other settings. See Figure 4 for an illustration counting the first four Catalan numbers.

Given: An RNA string ss having the same number of occurrences of 'A' as 'U' and the same number of occurrences of 'C' as 'G'. The length of the string is at most 300 bp.

Return: The total number of noncrossing perfect matchings of basepair edges in the bonding graph of ss, modulo 1,000,000.

Sample Dataset

>Rosalind_57
AUAU

Sample Output

2

 

 이 문제는 주어진 RNA 서열의 non-crossing match의 개수 즉 카탈란 수를 출력하는 문제이다. non-crossing match는 짝들을 선으로 이었을 때 서로 교차하지 않는 매치를 말한다. 모든 점이 서로 이어질 수 있다고 가정한다면, non-crossing match는 점화식을 이용하여 풀 수 있다. 

 예를 들어 1부터 8까지의 점이 있는 동그라미 모양의 서열을 생각해보자. 이때 1번 점을 기준으로 k번과 잇는다면, 1-k 쌍을 기준으로 2 ~ k-1과 k+1 ~ 8인 서열 두개가 나올 것이다. 우리가 구하려는 것은 non-crossing이므로 1-k를 잇는 선을 넘어가는 선을 그을 수는 없다. 그러므로 나뉜 두 서열 안에서만 다시 non-crossing 쌍을 구해야한다. 그러므로 길이가 8인 서열의 카탈란수는 2~k-1 서열의 카탈란수 곱하기 k+1~8 서열의 카탈란수가 될 것이다. 즉 점화식으로 구해진다. 

 필자는 처음에 점화식인지라 재귀의 방식을 이용하여 풀려고 했다. 하지만 주어진 서열이 못해도 300bp이상이라 시간이 너무 오래 걸리게 되었다. 인터넷에서 찾아본 결과 이런 경우에는 재귀뿐만이 아니라 다이나믹 프로그래밍을 응용하여 풀어야 한다고 깨달았다. 필자는 항상 다이나믹 프로그래밍에 고전하는 것을 보니 DP공부가 더 필요해보인다.

from Bio import SeqIO

def finding_CAT(s,node,cat_memo):#카탈란 찾기
    n=int(node/2)
    if n<=1:#길이가 2이하라면
        return 1
    if cat_memo.get((s,node),0):#이미 존재한다면
        return cat_memo[(s,node)]
    Cn=0
    for k in range(1,2*n,2):
        a,c,g,u=s[1:k].count('A'),s[1:k].count('C'),s[1:k].count('G'),s[1:k].count('U')#개수 세기
        if a==u and c==g and (s[0],s[k]) in [('A','U'),('U','A'),('G','C'),('C','G')]:
        	#AU,CG쌍 개수 같고, 지금 시작과 기준이 맞다면
            Cn+=finding_CAT(s[1:k],k-1,cat_memo)*finding_CAT(s[k+1:],2*n-k-1,cat_memo)#재귀
    cat_memo[(s,node)]=Cn#저장
    return Cn


ACGU={'A':'U','U':'A','C':'G','G':'C'}
if __name__=='__main__':
    with open(r'파일경로','r') as fa:
        S=next(SeqIO.parse(fa,'fasta')).seq

cat_memo={}
node=len(S)
cataln_number = finding_CAT(S,node,cat_memo)
print(cataln_number%1000000)