Introduction to Random Strings(무작위 문자열)

곰탱이장 2024. 8. 31. 09:17

ROSALIND | Introduction to Random Strings

It appears that your browser has JavaScript disabled. Rosalind requires your browser to be JavaScript enabled. Introduction to Random Strings solved by 4930 2012년 12월 4일 7:03:37 오전 by tvinar Topics: Probability Modeling Random Genomes We already

rosalind.info

Problem

Figure 1. The graph of the common logarithm function of x. For a given x-value, the corresponding y-value is the exponent to which we must raise 10 to obtain x. Note that x-values between 0 and 1 get mapped to y-values between -infinity and 0.

An array is a structure containing an ordered collection of objects (numbers, strings, other arrays, etc.). We let $A [k]$ denote the $k$ -th value in array $A$ . You may like to think of an array as simply a matrix having only one row.

A random string is constructed so that the probability of choosing each subsequent symbol is based on a fixed underlying symbol frequency.

GC-content offers us natural symbol frequencies for constructing random DNA strings. If the GC-content is $x$ , then we set the symbol frequencies of C and G equal to $\frac{x}{2}$ and the symbol frequencies of A and T equal to $\frac{1 - x}{2}$ . For example, if the GC-content is 40%, then as we construct the string, the next symbol is 'G'/'C' with probability 0.2, and the next symbol is 'A'/'T' with probability 0.3.

In practice, many probabilities wind up being very small. In order to work with small probabilities, we may plug them into a function that "blows them up" for the sake of comparison. Specifically, the common logarithm of $x$ (defined for $x > 0$ and denoted $\log_{10} (x)$ ) is the exponent to which we must raise 10 to obtain $x$ .

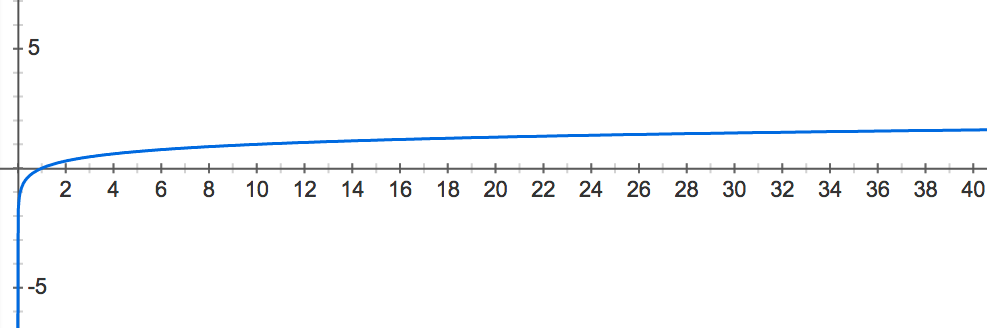
See Figure 1 for a graph of the common logarithm function $y = \log_{10} (x)$ . In this graph, we can see that the logarithm of $x$ -values between 0 and 1 always winds up mapping to $y$ -values between $- \infty$ and 0: $x$ -values near 0 have logarithms close to $- \infty$ , and $x$ -values close to 1 have logarithms close to $0$ . Thus, we will select the common logarithm as our function to "blow up" small probability values for comparison.

Given: A DNA string $s$ of length at most 100 bp and an array $A$ containing at most 20 numbers between 0 and 1.

Return: An array $B$ having the same length as $A$ in which $B [k]$ represents the common logarithm of the probability that a random string constructed with the GC-content found in $A [k]$ will match $s$ exactly.

Sample Dataset

ACGATACAA
0.129 0.287 0.423 0.476 0.641 0.742 0.783

Sample Output

-5.737 -5.217 -5.263 -5.360 -5.958 -6.628 -7.009

이 문제는 1개의 문자열이 주어지고 그 다음 A배열이 주어진다. A배열은 각각 GC 비율을 의미한다. B배열 k번째 인덱스는 A배열의 k번째 인덱스이 GC비율과 연관이 있다. GC비율에 따라 무작위 문자열을 만들었을때, 이 문자열이 주어진 문자열과 완전히 같은 확률이 B배열의 인자이다. 이 확률이 너무나도 작기에 상용로그를 씌워서 넣는다

import math

if __name__=='__main__':#직접 실행시
    with open(r'파일경로','r') as file:
        string=next(file).rstrip()#주어진 문자열
        A=list(map(float,(next(file).rstrip()).split()))#A배열

B=[]
for i in A:#i가 GC비율
    p=1
    pA,pC=(1-i)/2,i/2#A/T확률, G/C확률
    for s in string:
        if s=='A' or s=='T':
            p*=pA
        elif s=='C' or s=='G':
            p*=pC
    B.append(round(math.log10(p),3))#상용로그 씌우고 소수점3자리까지

print(*B)