백준 17070 파이프 옮기기 1

https://www.acmicpc.net/problem/17070

 

 이 문제는 파이프를 정해진 방식대로 밀어서 끝까지 가는 경로가 몇 개인지 구하는 문제이다. 

이 문제에서 파이프는 3가지 상태를 가지고 있다. 가로,세로,대각선이다. 그리고 이 세가지 상태에 따라 다음칸으로 움직일 수 있는 방법이 나뉜다. 가로의 경우에는 가로로 한칸 대각선으로 한칸, 세로의 경우에는 세로로 한칸 대각선으로 한칸, 대각선의 경우에는 가로로,세로로,대각선으로 한칸 움직일 수 있다. 이렇게 움직일 때 꼭 비어있어야 하는 칸들은 아래와 같다.

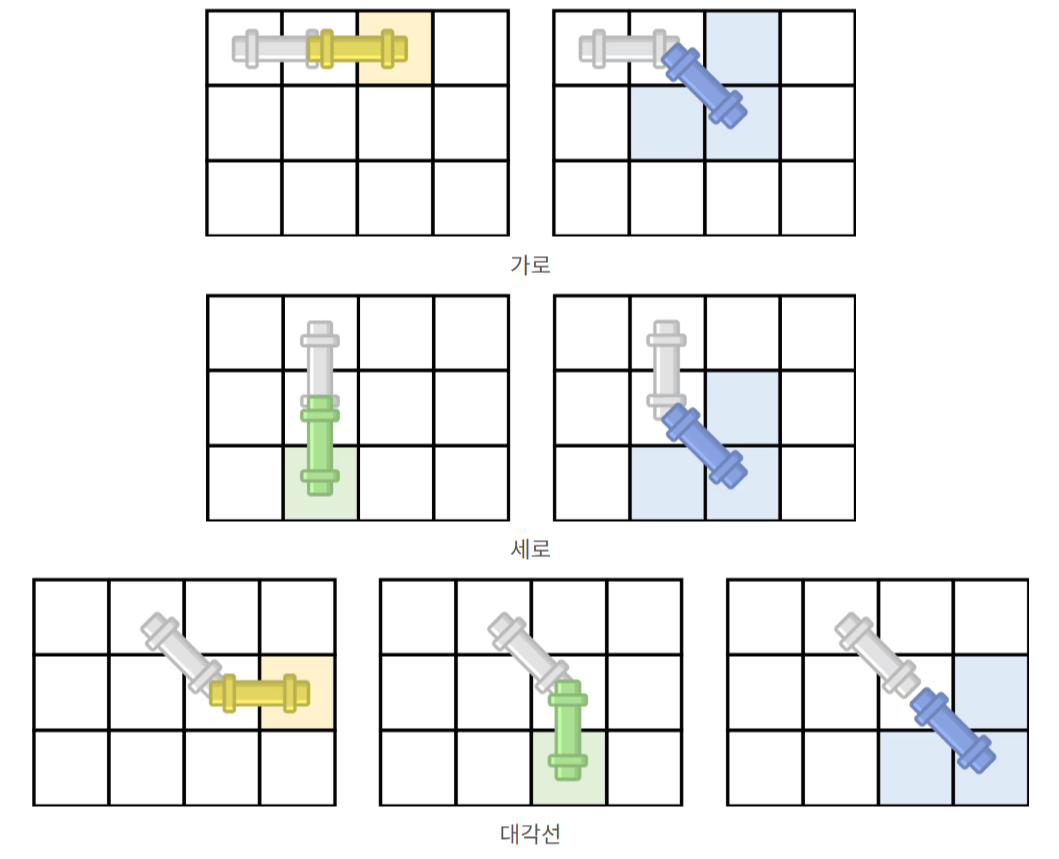
우리는 시작이 있고 끝으로 가는 경우의 수란 점에서 그래프 경로 찾기라는 걸 알게된다. 그렇다면 경로 찾기하면 BFS 아님 DFS인 것을 알 수 있다. 그런데 이 문제의 추가시간이 엄격한걸 보면 공간적으로 조금 손해더라도 시간복잡도가 중요하단 걸 생각해낼 수 있다. 이러한 방법에는 다이나믹 프로그래밍인 메모이제이션을 사용하여 기록하는 판 위에서 직접 기록하며 구해버리는게 직빵이다.

 우리는 이 문제에서 파이프의 상태를 가로 세로 대각선으로 나눠야 한다. 그러므로 필자는 메모이제이션한 배열 자체에서 [가로수,세로수,대각선수]로 표현하여 그 상태가 되는 경우의 수를 따로 기록하여 했다. 나머지는 조건을 따져가며 무슨 조건문 순서로 해야 가장 최적일까를 고민하며 차분하게 써내려가면 된다.

import sys
input = sys.stdin.readline

def DP():
    for r in range(N):
        for c in range(N):
            if graph[r][c]==1:
                continue

            if c+1<N and graph[r][c+1]!=1:#가로로 가능
                for idx,i in enumerate(dp[r][c]):
                    if idx!=1 and i!=0:
                        dp[r][c+1][0] += i
            
            if r+1<N and graph[r+1][c] != 1:#세로로 가능
                for idx,i in enumerate(dp[r][c]):
                    if idx != 0 and i !=0:
                        dp[r+1][c][1] += i
            
            #대각선으로 가능
            if r+1<N and c+1<N and 1 not in [graph[r+1][c+1],graph[r][c+1],graph[r+1][c]]:
                for i in dp[r][c]:
                    if i != 0:
                        dp[r+1][c+1][2] += i
    
    print(sum(dp[N-1][N-1]))

N=int(input().rstrip())
graph=[]
dp=[[[0,0,0] for j in range(N)] for k in range(N)]
for _ in range(N):
    graph.append(list(map(int,input().rstrip().split())))

dp[0][1][0]=1

DP()